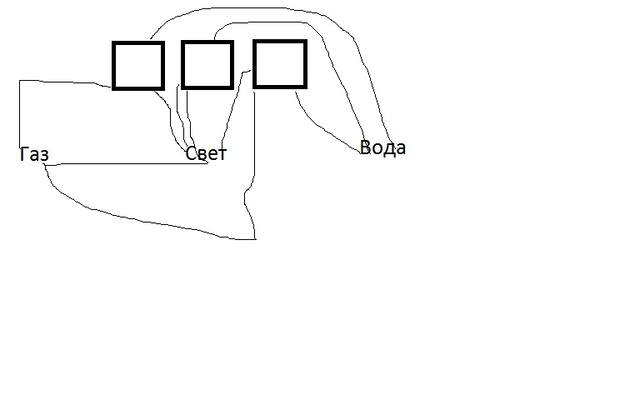
Супер загадка.
-
задача не решаема в линейном виде и решить ее можно только с помощью 3D технологии. Жду Голосов!!!
-

-
**-NegaTiv-** %(red)[**задача не решаема в линейном виде и решить ее можно только с помощью 3D технологии. Жду Голосов!!!**]Я это ему в личку 100 лет назад написал.
И он говорит это неправильно. -

-
Kovcheq, я уже рисовал такую
-
Я разгодал!
-
**e6u_na_letu** Я разгодал!Скрин где?!
-
Согласно теореме Эйлера 1752 года, задача решения не имеет. Правда, в случае Эйлера, он брал трех соседок и соединял их с тремя колодцами (нет, не топил).
ЗЫ: Если не брать за основу двухмерную плоскость, а взять трехмерную, то тогда да, можно всем провести и газ, и воду, и свет.
Добавлено через 00:29 мин.
с тебя 100 голосов инф а 100% -
[spoiler=ответQ: Задача Эйлера. Три соседа поссорились. Все три имеют по колодцу. Возможно ли проложить тропинки от дома каждого соседа к каждому колодцу так, чтобы эти тропинки не пересекались?
A: В двухмерном пространстве невозможно соединить три колодца тропинками так, чтобы они не пересекались.
Теорема имеет непросредственное отношение к теории графов. Решений за 300 лет, прошедших с формулировки задачи о колодцах, нашли не одно - вот пара:
- заключается в рассмотрении трех вариантов, остающихся после проведения 8ми тропинок.
Решение: Обозначим вершины графа А, B, C, 1, 2, 3 соответственно трем домикам и колодцам формулировки задачи, и докажем, что девятую дорогу - ребро графа, не пересекающюю другие ребра, провести невозможно.
Проведенные в графе ребра А-1, А-2, A-3 и В-1, В-2, В-З (соответствующие дорожкам от домиков А и В ко всем трем колодцам). Построенный таким образом граф разделил рабочую плоскость на 3 области: X, У, Z. Вершина B, в зависимости от ее расположения на плоскости, попадает в одну из таких 3х областей. Если рассмотреть каждый из 3х случаев «попадания» вершины B в одну из областей X, Y, Z - то увидите, что всякий раз какая-нибудь одна из вершин графа 1, 2 или 3 (или один из колодцев "соседей") получится недоступной для построения дороги от вершины B (т. е. невозможно будет построить одно из ребер B1, B2 или B3. которое не пересекло бы уже имеющиеся в графе ребра). Соответственно - ответ - нельзя!
2.основываясь на соотношении того же Эйлера для многоугольников
Решение: Предположим, что эти 9 тропинок можно проложить. Обозначим домики точками H1, H2, H3,колодцы - точками C1, C2, C3. Каждую точку-дом соединим с каждой точкой-колодцем. Получились ребра (графа) в количестве девяти штук, которые попарно не пересекаются. Такие ребра образуют на рассматриваемой плоскости задачи многоугольник, поделенный на меньшие многоугольники. Для такого разбиения должно выполняться известное соотношение Эйлера B - P + G = 1. Добавляем к рассматриваемым граням еще одну - внешнюю часть плоскости относительно рассматриваемомого многоугольника. Тогда соотношение Эйлера примет вид B - P + G = 2, причем B = 6 и P = 9. Получается, G = 5. Каждая из пяти граней имеет по крайней мере четыре ребра, так как, по условию задачи Эйлера, ни одна из дорожек не должна напрямую соединять два колодца или два дома. Так как любое ребро лежит ровно в 2х гранях, то кол-во ребер графа должно быть не меньше 5*4/2 = 10. Это противоречит условию исходной задачи, по которому их число равно девять! Полученное противоречие доказывает, что ответ в задаче о 3х колодцах Эйлера отрицателен.
Решение "можно" получается при переходе в трехмерное пространство, либо при вспоминании того факта, что Земля - круглая, либо "замараживании" высокого уровня воды в одном из колодцев и предположения что по льду можно ходить, либо при "строительстве" мостов, туннелей и т.п. .[/spoiler]]
-
Да минусуем ему репу. Он кидала многии уже решили , а он не дает 100 голосов.
-

-
мда я наёбка он вам голоса не даст
-
Идем в газпром и просим чтоб у нас в деревне занесли газ свет и т.д.
-
Не реально решить. Там газ сделаешь, и в 2 дома свет. Остальное нереально.